LOAM: Lidar Odometry and Mapping in Real-time
1.introduction
- LOAM分为两个算法:
- Odometry:高频低保真用来估计速度
- Mapping:低频高保真用来精确匹配以及定位
- 假设以及前置条件
- 扫描速度»运动速度时 失真可以忽视
- lidar校准准确
- lidar角速度及线速度平滑连续
- 定义
- $k,k\in Z^+$表示某次扫描
- $P_k$表示第k次扫描生成的点云
- ${L}$表示一个三维坐标系,坐标系的$(0,0,0)$为lidar的几何中心
- $X^L_{(k,i)}$表示在${L_k}$中的点$i\in P_k$的坐标coordinates
- ${W}$表示一个三维坐标系,坐标系的$(0,0,0)$为lidar的初始位置
- $X^W_{(k,i)}$表示在${W_k}$中的点$i\in P_k$的坐标coordinates
- P^ 是laser每次扫描映射到${L}$中的点
- CW顺时针,CCW逆时针
- $E_{k}$为k时的边缘点集合
- $H_{k}$为k时的平面点集合
- 术语
- 6-DOF: 6自由度
- KD-tree K维树用来组织表示 K 维空间中点集合,它是一种带有其他约束条件的二分查找树。
- skew symmetric matrix 斜对称矩阵
- diag()对角阵
2.overview
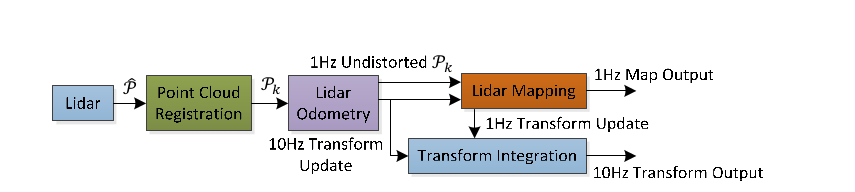
- Point Cloud Registration :第k次完整扫描sweep
- LidarOdometry : 计算lidar两次扫描,以矫正运动带来的$P_k$失真,算法以10Hz左右的频率运行.再将校正后的$P_k$以1Hz的频率输出
- Lidar Mapping 绘制地图
- Transform Integration :将来嗯个算法的P进行变换积分,生成10HZ的{W}信息.
3.Lidar Odometry
a.特征点提取
-
实验使用的激光雷达以$180^◦/s$的角速度旋转,扫描频率为40HZ,因此垂直于扫描平面的分辨率为$180^◦/40=4.5^ ◦$,一次扫描有着共面关系
-
特征点选择边缘与平面上的,$i\in P_k$,$S$是一次扫描返回的i的连续集合,$S$在$i$的每一侧包含一半的点.
-
平滑度计算公式(1)
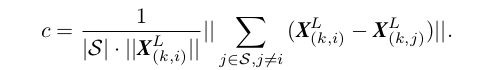
周围多个点坐标(x,y,z)求和在比上总点数乘i点坐标.
c越接近1表示越平滑.大于1突出比平均水平,小于1凹陷比平价水平
c最大的点作为边缘点
c最小的作为平面点
平面分为四个区域
每个区域最多提供2个边缘点和4个平面点
只有超过某个阀值才进行选择 - 不希望得到的点:
- 被包围的点(选择的点周围点不能在被选中)
- 与激光素大致平行表面上的点. (a)图B点
- 遮挡区域边界上的点(某些视角可见某些不可见) (b)图A点
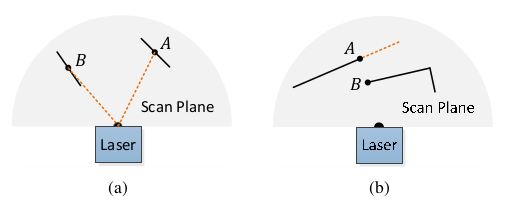
- 每个区域不能超过边缘点/平面点最大值
B.Finding Feature Point Correspondence 找特征点关系
-
$P_k$被重新投影到时间戳$t_{k+1}$下记为$\vec{P_k}$在K+1期间与$P_{k+1}$一同估计激光雷达运动
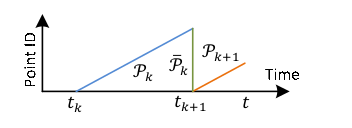
找$\vec{P_k}$与$E_{k+1}$和$H_{k+1}$的对应关系
$t_{k+1}$时$P_{k+1}$是空集 -
第K+1次迭代的开始会利用第K次的6-DOF运动估计将$E_{k+1}$和$H_{k+1}$重新投影为$\vec{E_{k+1}}$和$\vec{H_{k+1}}$(重投影集)
$\vec{E_{k+1}}$和$\vec{H_{k+1}}$(重投影集)中的每一个点将在$\vec{P_k}$寻找附近的点
注:$\vec{P_k}$存在一个3d-tree内以便快速查找 - the procedure of finding an edge line as the correspondence of an edge point(特征点) in $\vec{E_{k+1}}$(a).
- $i\in \vec{E_{k+1}}$ ,$j\in \vec{P_k }$ , $j$是$i$的最临近点
- let l be the closest neighbor of i in the two consecutive scans to the scan of j.(j, l)
(边缘线edge line)forms the correspondence of i(边缘点edge point). - 前置条件: scan cannot contain more than one points from the same edge line.
- 验证:通过(1)式来验证j,l是否为边缘点
- the procedure of finding a planar patch as the correspondence for a planar point in ̃$\vec{H_{k+1}}$(b).
- $i\in \vec{H_{k+1}}$ ,$j\in \vec{P_k }$ , $j$是$i$的最临近点,与procedure of finding an edge line 相同.
- $l\in \vec{P_k}$ 在与j的同一次扫描中
- let m be the closest neighbor of i in the two consecutive scans to the scan of j
- 验证:通过(1)式来验证点i,j,m的共面性
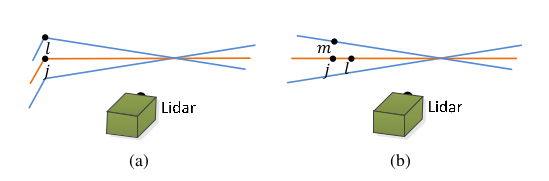
注:桔黄色线代表对j的一次扫描,蓝色线代表两次连续扫描 - 计算特征点i到对应的edge line[j,l]的距离
距离$dE$满足下(2)式,将通过最小化最小化特征点总距离来恢复激光雷达运动
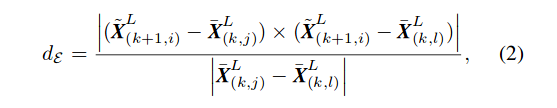
分子为$\vec{ji},\vec{li}$构成平行四边型面积,是三角形$ijl$的两倍. - 点到平面距离满足下(3)式
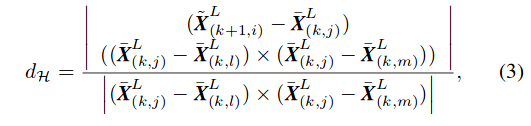
分子为$\vec{ji},\vec{lj},\vec{mj}$构成平行六面体体积.分母为底面积,二者之比为点$i$到平面$lmj$距离
C.Motion Estimation移动估计
- 定义
- 记 $t$ 为当前时间, $t_{k+1}$ 为第k+1次扫描开始
- $T^L_{k+1}=[t_x,t_y,t_z,\theta_x,\theta_y,\theta_z]^T$ is lidar pose transform between$[t_{k+1},t]$,$T^L_{k+1}$是6-DOF六自由度的刚性运动在
- $t_x,t_y,t_z$是在${L}$中沿着$x,y,z$ axes轴的translation平移
- $\theta_x,\theta_y,\theta_z$是旋转角度,符合右手定则
- $i,i\in P_{k+1}$ , $t_i$是i的时间戳
- $T^L_{(k+1,i)}$be the pose transform between$[t_{k+1}, t_i]$
- $E_{k+1},H_{k+1}$是从$P_{k+1}$中提取的边缘点及平面点集合
- $\vec{E_{k+1}},\vec{H_{k+1}}$是重新投影到开始时间戳,如[t,t+1]扫描完了投影到t时间点
- $T^L_{(k+1,i)}$可以通过$T^L_{k+1}的线性插值来计算,公式(4)如下:
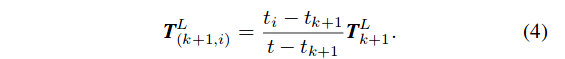
- 应用(4)可以建立$E_{k+1},H_{k+1}$到$\vec{E_{k+1}},\vec{H_{k+1}}$的几何变换公式(5)如下:
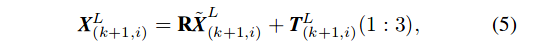
注:- $X^L_{(k+1,i)}$是$i$在$E_{k+1}$或$H_{k+1}$中的坐标 , $\vec{X^L_{(k+1,i)}}$是对应点在$\vec{E_{k+1}},\vec{H_{k+1}}$中的坐标
- $i$是过程中的一个点
- $T^L_{k+1}(1:3)$是指$T^L_{k+1}$矩阵的前三行
- R是Rodrigues公式定义的旋转矩阵

- $\theta$是旋转的大小,是旋转向量的绝对长度
- $\omega$是旋转的单位方向
- $\vec{\omega}$是$\omega$的斜对称矩阵
- 结合(2)和(4)-(8)可以得到边缘点与边缘线之间的关系
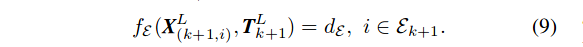
通过k+1次扫描中的一个特征点i,k+1到现在的位置改变,得到边缘点到线的距离 - 结合(3)和(4)-(8)可以得到平面点与平面之间的关系
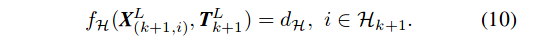
通过k+i次扫描中的一个平面点i,以及k+1次扫描到现在的位置改变,获得i到其对应平面的距离 - 结合(9),(10)可以得到代价函数:
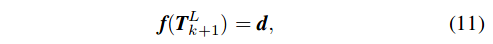
位置变换的代价函数,可以验证位置变换的正确性 - 计算$J=\partial f/\partial T^L_{k+1}$ 通过非线性最小二乘法,将d下降到0
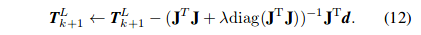
$J$为列向量$J^TJ$为一个数伪代码

该算法每次扫描调用多次
15行权重分配策略,距离较大的用较小权重分配,距离大于阀值的视为异常值使用0权重
16行更新一次T,查看是否收敛或满足最大迭代次数
21行如果扫描结束则返回矫正映射到$t_{k+2}$处的点云,否则只返回T进行下一次递归
LIDAR MAPPING
###定义
- 在k+1次扫描结束时 Odometry算法产生无畸变点云$\vec{P_{k+1}}$,同时得到了$[t_{k+1},t_{k+2}]$之间的位置偏移$T^L_{k+1}$
- 匹配算法将$\vec{P_{k+1}}$匹配到世界坐标中成为$\vec{Q_{k+1}}$
- $T^W_k$为k次扫描结束时lidar在世界坐标中的姿势
- $Q_k$为世界地图中积累到K次扫描结束的点云,程序中为10立方米的区域.
- 利用$T^W_{k+1}$将$\vec{Q_{k+1}}$与$Q_k$匹配,以获得$Q_{k+1}$
- $\vec{Q_{k+1}}$与$Q_k$相交的点被保存到3d-tree上
- $S’,S’\in Q_k$为特征点周围的点
- $M$为$S’$的协防差矩阵
- $V$是$M$的特征值,$E$是$M$的特征向量
算法
- 确定方向:(PCA方法)如果$S’$在边缘线上,V包含了两个很大的特征值,E中与最大特征值关联的特征向量表示边缘线方向
特征值是投影后数据保留的量,而特征向量就是投影到的基向量 - 确定方向:(PCA方法)如果$S’$在平面上,E中与最小特征值关联的特征向量表示边缘线方向即是平面法线的方向
- 确定位置:通过$S’$的几何中心确定